Anaqsim Modeling Concepts

This section does not repeat details that are published elsewhere in books and articles, but instead gives a quick outline of the techniques used in Anaqsim and cites the appropriate references for those interested in the details.

Anaqsim employs the analytic element method (AEM), which superposes analytic solutions to yield a composite solution consisting of equations for head and discharge as functions of location and time.  The AEM is described in detail in books by Strack (1989) and Haitjema (1995).  Shorter summaries of the method may be found in Fitts (2023) and Strack (2003).  The AEM is fundamentally different than numerical methods like finite elements and finite differences, where the domain is broken into small blocks or elements and simple head distributions (e.g. linear) are assumed within these blocks or elements.  In the AEM, boundaries of the domain are discretized, but the domain itself is not.

Anaqsim uses a variation of the AEM that divides the modeled region into subdomains, each with its own definition of aquifer parameters and its own separate AEM model (Fitts, 2010).  The model for a given subdomain (called a domain in Anaqsim) includes contributions from elements inside and on the external boundary of the subdomain; elements beyond the subdomain do not contribute.  Each subdomain model is written in terms of two-dimensional functions, but three-dimensional flow may be simulated using multiple levels in a model.  In multi-level models, the resistance to vertical flow is accounted for in the vertical leakage between levels.

This subdomain approach allows for a high degree of flexibility with respect to a model's heterogeneity, anisotropy, and layering.  For example, it is possible for a subdomain that is anisotropic to be adjacent to another subdomain that is isotropic or anisotropic with a different direction and ratio.  The subdomain approach allows mixed layering schemes.  For example, an area with multiple levels (subdomains stacked vertically and leaking vertically to each other) can abut an area with subdomains in just a single level.  This allows the model to focus layering and computational effort in the area of interest, with a simpler single-level model for distant areas.

Another key aspect of Anaqsim is that it allows complete transient simulation capabilities by using finite difference time steps as suggested by Haitjema and Strack (1985).  The transient term in the flow equations is handled in essentially the same manner as it is in finite difference programs like MODFLOW.

Subdomains and Model Levels

Anaqsim uses one separate two-dimensional model for each subdomain. In Anaqsim, subdomain input is entered in the Model Input / Domains data tables (Domain in Anaqsim's menu system is short for subdomain).  In each subdomain model, the resistance to vertical flow is neglected and the head is independent of elevation within the subdomain (Dupuit assumption).  Resistance to vertical flow and three-dimensional flow are modeled by using multiple levels with vertical leakage between levels.  To illustrate how subdomains and model levels are implemented in Anaqsim, we will go through several examples, starting from simple and working toward complex.

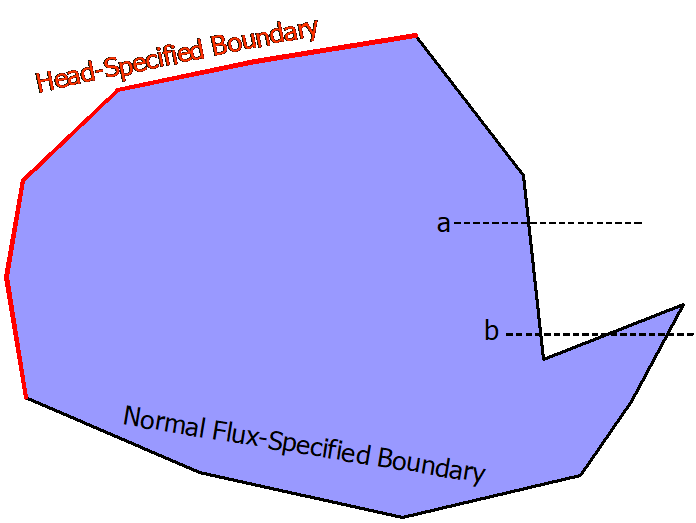
The simplest model would be one level (two-dimensional), and only one subdomain (homogeneous).  A plan view of such a simple model is shown below.

The properties of the subdomain (hydraulic conductivity, porosity, elevations, etc) are defined in the Model Input / Domains menu.  The spatial extent of the subdomain (blue) is defined by the line boundaries that are listed as being on the external perimeter of the subdomain.  This is different from TWODAN or other analytic element programs where one domain is the infinite "background" domain, and a heterogeneity (domain) lies inside a polygon dedicated to defining the heterogeneity boundary.  The scheme in Anaqsim allows different kinds of boundaries to define the limits of a domain, which is much more flexible.  In the simple model shown above, there are two line boundaries that form the external boundary of the domain: one that is head-specified (red) and one that is normal-flux specified (black). 

The algorithm that determines what points lie inside the domain works as follows:  a point is inside the subdomain if going in the positive x direction (right) from the point, you cross a boundary of the domain an odd number of times.  For most points inside the domain, there is only one boundary crossing in the positive x direction (like "a" above), but it is possible to have three or more crossings (like "b" above).

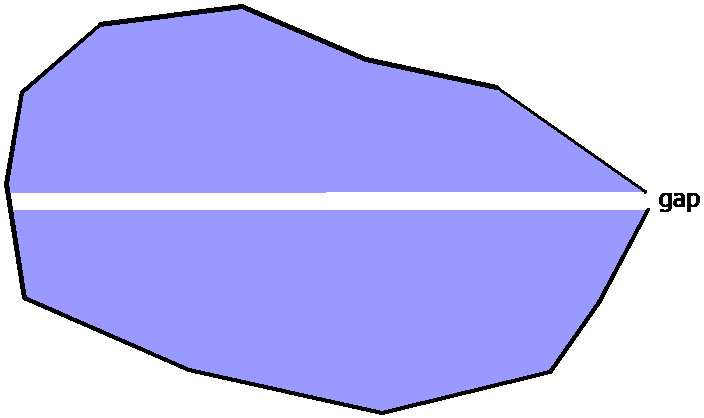
In general, subdomain boundaries should combine to form a perfectly closed polygon, with exactly matching points where the line boundary end/start points meet.  If the line boundaries defining the boundary of the domain have a gap, it can lead to erroneous definitions of domain areas and odd model results.  The boundary gap in the example below allows a strip to the left of the gap (white) that is technically not inside that domain (blue); points in this strip have zero boundary crossings to the right.  A similar result happens if there is overlap in the location of two end/start points; where they overlap, the algorithm sees two crossings in the positive x direction.

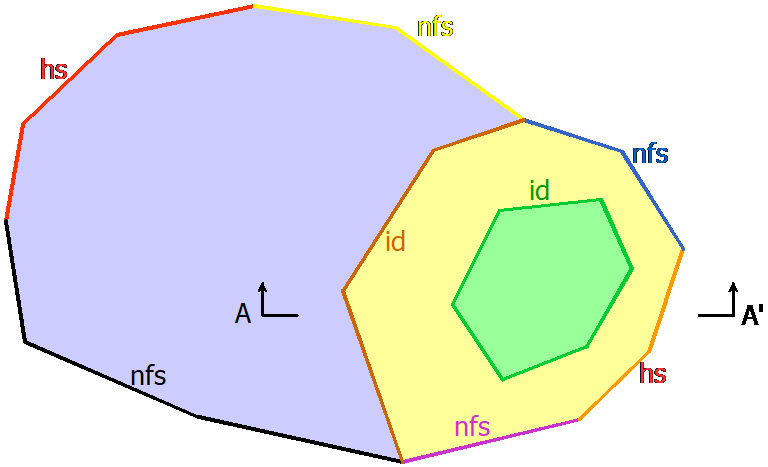
Now consider a model that is still one level (two-dimensional), but is heterogeneous with three subdomains, blue, yellow, and green (below).  This example has three types of line boundaries which are labeled: head-specified (hs), normal flux-specified (nfs), and inter-domain (id).  Each different line boundary is shown in a different color and is labeled hs, nfs, or id.  At all the common intersections where two or more line boundaries meet, the coordinates of the end points must match exactly, so that each subdomain region is defined without gaps or errors.

Along inter-domain boundaries, you specify which domain lies to the left and which domain lies to the right.  For example, if the coordinates of the inter-domain boundary between blue and yellow are listed in order from bottom to top, blue is to the left and yellow is to the right.  If the coordinates of the boundary between yellow and green is defined in clockwise order, yellow is to the left and green is to the right.

Now imagine that the model shown above is a single level in the blue and yellow areas (two-dimensional), but has four levels in the green area (three-dimensional).  A vertical  cross section along A-A' for such a model is shown below.

The convention for naming levels in Anaqsim is to start at level 1 at the top and increase the level numbers with depth in a multi-level stack.  In the green area, level 1 is at the top and level 4 is at the bottom.  Anaqsim assumes that there is vertical leakage between subdomains that exist in the same area but at different vertical levels.  It is possible to skip a level number in a stack of subdomains; for example, the green area in the above section could have domains with levels 2,3,5 and 6 rather than levels 1,2,3 and 4.  Anaqsim finds the next domains above and below, no matter what the level numbers are and even if there are gaps in level numbers.  This is helpful in cases with complex layering schemes such as where a domain has limited extent compared to the domains above and/or below it.  The resistance to vertical flow between levels is computed based on the vertical hydraulic conductivities and thicknesses specified for the domains involved.

The brown inter-domain boundary separating the blue and yellow subdomains would have one subdomain on the left (blue) and one on the right (yellow).  The green inter-domain boundary separating the yellow and green subdomains would have one subdomain on the left (yellow) and four on the right (shades of green), assuming that boundary is defined with coordinates in clockwise order.  Across inter-domain boundaries, there is approximate continuity of head and approximate continuity of the normal component of discharge.  This approximation is discussed more in the Line Boundary Conditions section.  Interdomain boundaries can connect subdomains in different levels (e.g. level 1 on one side and levels 2 and 3 on the other).

Left / Right with Respect to Line Boundaries

With interdomain line boundaries and with normal flux-specified line boundaries, it is important to specify boundaries to the left and/or to the right of the line boundary.  To explain what this means, refer to the following figure.

Assume that north is up and south is down in this map-view plot of an Anaqsim model.  The different colored areas represent different subdomains, which are bounded by various line boundaries.  Consider the red interdomain line boundary (id) that separates the blue and yellow subdomains.  If the coordinates for this line boundary are in order from south to north, then the blue subdomain would be to the left and the yellow subdomain would be to the right.  Think of it as though you were walking along the line boundary from the first vertex towards the last vertex in the coordinates.  The "left" side is to your left as you walk along the boundary and the "right" side is to the right.  Alternatively, if the coordinates of this interdomain boundary are listed in order from north to south, then the yellow domain is to the left and the blue domain is to the right.

Now consider the green interdomain boundary separating the green and yellow subdomains.  If the coordinates of that boundary are specified in clockwise order, the yellow domain is to the left and the green domain is to the right.  Alternatively, if the coordinates of that boundary are specified in counter-clockwise order, the green domain is to the left and the yellow domain is to the right.

When a normal flux-specified boundary is external or with a head-dependent normal flux boundary, the vertex coordinates must be specified in counter-clockwise order, with the domain to the left of the boundary as you proceed along it.   Consider the purple normal flux-specified boundary (nfs) in the figure.  It's coordinates must be specified in counter-clockwise order (west to east) with the yellow domain to the left.  Likewise, for the blue normal flux-specified boundary, the coordinates must be specified counter-clockwise from southeast to northwest, keeping the yellow domain to the left.  The normal flux is positive for flow across the boundary from left to right as you proceed from the start toward the end (flow out of subdomain).  Normal flux is negative for flow from right to left as you proceed from the start toward the end (flow into subdomain).  

Recharge, Leakage and Transient Storage

Like in any flow model, the flow equation in Anaqsim is based on Darcy's Law and conservation of mass (and volume, with constant density).  The conservation equation, in its simplest is:

where ∇Q is the divergence of the two-dimensional aquifer discharge vector field and  γ is the net extraction per area (sink term, units of L/T).   The sink term γ may have contributions from leakage out the top of the subdomain (L_t),  leakage out the bottom of the subdomain  (L_b), and  transient discharge/area into storage(S ∂h/∂t) .  See equations 4-6 of Fitts (2010).

The vertical leakages L_t and L_b are specific discharges proportional to the head difference between the domain and the head above or below (could be specified head or another domain at a different level), and proportional to the equivalent vertical hydraulic conductivity K_e that is based on the vertical conductivities and the saturated thicknesses at the average heads specified for the domains involved.  If there is leakage between two domains at different levels, the equation used for computing K_e is

where b1 and b2 are the average saturated thicknesses of the two layers and K1 and K2 are the vertical hydraulic conductivities of the two layers.  In Anaqsim, K_e is assumed to be constant and independent of head and actual saturated thickness.
Under restricted circumstances (uniform recharge, steady flow, and a single-level model), γ is constant and independent of location.  In such cases, the uniform γ distribution may be modeled exactly using a uniform area sink.

In many practical cases, the model needs spatially-variable extraction (γ varies with x, y) due to spatially-variable vertical leakage and/or spatially-variable storage changes.  When that is the case, the model needs spatially-variable area sinks to approximate the proper distribution of γ.  The spatially-variable area sink functions in Anaqsim create a smooth, continuous, irregular γ surface within a subdomain.  The model is using equation 13 of Fitts (2010) as a model of the distribution of γ, with γ equal to the perfect extraction/area (computed by equation 6 of Fitts (2010)) at each basis point, but approximating equation 6 of Fitts (2010) between basis points.  The modeled distribution of γ satisfies the flow equation perfectly at basis points and approximates the flow equation between basis points.  This approximation is more accurate if the basis point spacing is smaller.

To check the accuracy of this approximation, Anaqsim provides an analysis tool (Analysis Menu / Conditions Along a Line).  If checks with this tool reveal a poor approximation, the basis point spacing is too large.  If the approximation is fine, you may be able to decrease the basis point spacing and save some computation.

Spatially-variable area sinks can rack up a large number of equations and computational burden on the system, so use them sparingly.  Where possible (often the far-field), use a single level in the model, which if it is steady means you can use the very efficient uniform area sinks instead of spatially-variable area sinks.  Use the special well basis point spacings around wells to gain accuracy with minimal computation.

Elements

The analytic elements used in Anaqsim include the elements described in the following references:

• The standard well element described by Strack [1989] is used in isotropic subdomains and the well element of Fitts [2006] is used in anisotropic subdomains. 
• Line boundaries are represented by high-order line elements similar to those described by Jankovic and Barnes [1999].  Line elements are either linesinks, line dipoles, or line doublets.  Line elements may have up to ten unknown parameters (degrees of freedom).  For example, a linesink with one parameter has a constant discharge/length along its length, a linesink with two parameters has discharge/length that varies linearly along its length, and a linesink with three parameters has discharge/length that varies parabolically along its length.  Strack [1989] gives a good overview of line elements.
• Uniform area source/sinks (constant over a subdomain) are modeled with the uniform recharge functions described by Strack [1989]. For these, the extraction/area is uniform over the entire subdomain.  This is appropriate in cases with a single level, steady flow, and a uniform recharge rate or zero recharge.
• Spatially-variable area source/sinks are modeled with the multi-quadric radial basis function elements described by Strack and Jankovic [1999].  With these, the extraction/area varies with location.  Spatially-variable extraction occurs when the extraction = recharge  + leakage + transient storage flux is spatially variable.  This is generally the case in multi-level models where spatially-variable leakage occurs and in transient models where spatially-variable storage flux occurs.  See the previous section and Fitts (2010) for details of how these elements are used to represent recharge, leakage and storage flux.

Wells

There are three possible kinds of pumping wells in Anaqsim:

1. Discharge-specified wells in just one subdomain.  With this type of well, you specify the known discharge of the well.
2. Discharge-specified wells spanning multiple subdomains.  This is for wells that are screened across multiple levels and subdomains in a multi-level part of a model.  For example, a well could be screened across the two lowest levels in a 4-level part of a model.  You specify the known discharge of the well, and Anaqsim imposes these conditions:  a) the heads at the well radii in each screened subdomain are identical, and b) the total discharge of the well elements in the screened subdomains equals the specified discharge of the well.
3. Head-specified wells in just one subdomain.  With this type of well, you specify the known head at the well radius.  Anaqsim determines the discharge needed to meet this condition.

Interdomain Line Boundary Conditions

At the inter-domain boundaries, two different boundary conditions are enforced by Anaqsim.  First, heads are matched across the boundary at specific points in all subdomains that intersect the boundary.  For example with the green inter-domain boundary shown in the figures below, heads are matched in the yellow domain and the four green domains at control points along the boundary.

Plan view (above) and section view (below) of a multi-domain model.

Secondly the normal component of discharge is matched across line segments on the inter-domain boundary. For the green inter-domain boundary, this means that the sum of the normal components of discharge in the four green subdomains must equal the normal component of discharge in the yellow subdomain.  This condition is enforced across intervals on a line segment.  If each line segment on the inter-domain boundary has n parameters, then the condition is enforced across n intervals per line segment.

A good way to check that you have enough parameters specified on any line boundary condition is to use right-click/ Check Line Boundary Conditions, which creates a plot of the boundary condition accuracy along a line segment of the line boundary.  If you don't have satisfactory accuracy, you can either (1) go under Line Boundaries and specify more parameters (control points) per boundary line segment, and/or (2) break a long boundary line segment into multiple, shorter segments.

One consequence of the head-matching condition is that there will be no vertical hydraulic gradient between different levels on the multi-level side of an inter-domain boundary.  This is consistent with the fact that there is no vertical resistance to flow accounted for on the single-level side of an inter-domain boundary.  Because of this, it is not appropriate to use one inter-domain boundary with multiple levels on both sides of the boundary; doing so would remove vertical head gradients at the boundary, which defeats the purpose of having multiple levels.  

With inter-domain boundaries, there should generally be just one domain (level) on one of the two sides of the boundary.  Anaqsim checks the input and gives a warning if there are two or more levels on both sides of an inter-domain boundary.  To explain why, consider the case illustrated below, with two levels on the yellow side of the inter-domain boundary(s) and four on the green side.  If there was just one inter-domain boundary there, it would be as though an infinitely conductive thin vertical boundary were inserted  between the yellow side and the green side, and heads would match in all six domains that meet there, meaning there can be no vertical head gradient on either side of the boundary.  The total normal component of discharge would match (total normal discharge in the two yellow domains would match the total normal discharge of the four green domains), but that normal discharge may be distributed oddly between different levels (e.g. a lot of flow from the lower yellow level going into the uppermost green level).  A better solution would be to use two inter-domain boundaries:

1. one with the lower yellow domain on one side and the two lowest green domains on the other, and
2. one with the upper yellow domain on one side and the upper one or two green domains on the other.  

This way, there can be vertical gradients between the yellow/green interface, and upper-level flows are matched with each other and lower-level flows are matched with each other.

Pathline Tracing

Pathlines are traced in the horizontal plane using the aquifer discharge vector function in the domain and a numerical tracing procedure outlined in section 26 of (Strack, 1989).  Three-dimensional pathline tracing is done using a finite-difference form of equation 24 in the paper by Strack (1984), which uses three-dimensional flow continuity to approximate the vertical component of pathlines.  For transient models, pathlines are traced through a transient flow field that evolves through the duration of the transient simulation (this is new in release 2016-2; earlier releases traced pathlines through the flow field of the last time step in a transient model).  From release 2016-2 on, pathlines in transient models start at the specified start time, and can be traced backward to the beginning of the simulation or forward until the end of the simulation.  In steady models, pathlines are traced forward or backward until they either exit the model or until the specified total time is reached.

Where pathlines cross inter-domain boundaries, the elevation of the pathline is adjusted so that the fraction of the normal component (perpendicular to the boundary segment) of flow above and below the pathline on each side of the inter-domain boundary match.  For example, say you have an inter-domain boundary with one domain on the left and three on the right.  If the pathline comes to the boundary from the left with 45% of the normal component of discharge above the pathline and 55% below it, the domain and elevation of the pathline side will be determined so that this 45/55 ratio is preserved on the right side as well.  There is typically a jump in the elevation of the pathline as it crosses an inter-domain boundary for the following reasons:

• The elevations of the domains on left and right do not necessarily match
• Where there are multiple levels on one side of the boundary, the distributions of the normal components of flow vary from one level to another due to K and flow field variations
• The total normal components of flow match only approximately from left to right side (see Fitts (2010)).  Anaqsim is not matching these normal components of flow perfectly at every point on the boundary - it is matching the total normal discharge across segments of the boundary perfectly.  

When the normal discharge components across an inter-domain boundary are in different directions in different levels (usually where flow is nearly stagnant) this algorithm breaks down, and under such conditions pathlines may terminate at the inter-domain boundary.

When pathlines intersect an internal line-sink boundary such as a river boundary, there are two possibilities: 1) the pathline could be consumed by the linesink and terminate, or 2) the pathline could continue on underneath the linesink.  Whether option 1 or 2 occurs is determined based on the elevation of the pathline as it approaches the linesink, the discharge/length of the linesink at the intersection, and the normal component of the domain discharge at the intersection.  It is assumed that the linesink is at the top of the domain and draws its water from the upper portion of the domain discharge.  If the result is case 2 with the pathline continuing under the linesink, its elevation will generally jump as it crosses under the linesink, gaining elevation if the linesink is extracting water and losing elevation if the linesink is injecting water.

In multi-level areas of models, pathlines can cross from one level to another vertically.
Where pathlines exit the bottom or top of the model due to recharge or leakage (e.g. at the water table for pathlines traced upstream), Anaqsim draws a circle at the end of the pathline and if you move the cursor over the circle, it will display elapsed time, domain, elevation, etc.